Three Geometry Problems on Maxima and Minima

Exercise 1

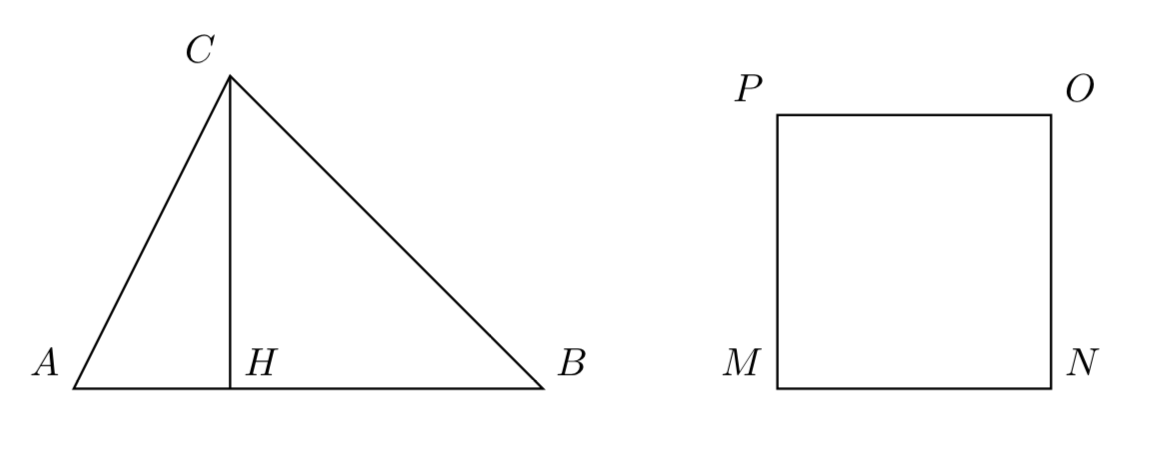
A square and a triangle have the same area. Which shape has the greatest perimeter?

Hint
It may be useful to remember the following formula:

Arithmetic Mean-Geometric Mean Inequality
Let \(x_{1},x_{2}, \dots x_{n}\) be non-negative real numbers; then:

\[ \dfrac {x_{1}+ x_{2} + \cdots x_{n}}{n} \ge \sqrt[n]{ x_{1}x_{2} \cdots x_{n}} \]

Solution
The triangle has the greatest perimeter.

Exercise 2

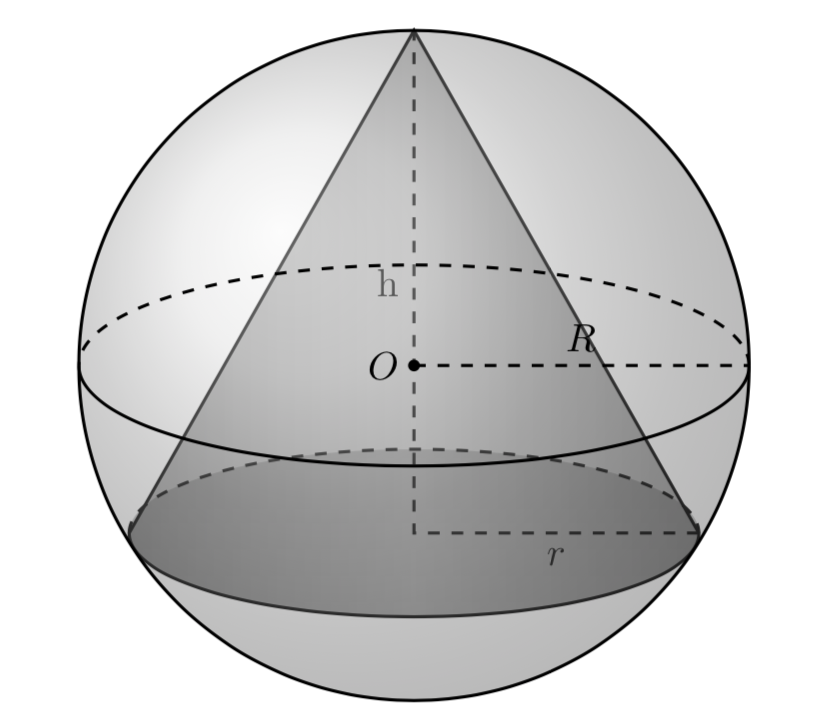
Let \(S\) be a sphere of fixed radius \(R\). Determine the height of the inscribed cone of maximum volume.

Solve also without using calculus (first derivative test).

Solution: [ \( h=\frac{4R}{3} \) ]

Exercise 3

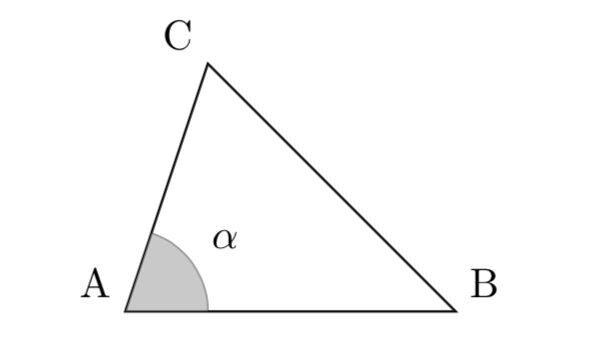
Let \(T\) be the set of all the triangles \(\triangle ABC\), which have a fixed angle \( \alpha\) in the vertex \( A\) and a fixed area \(S\). Show that the one with the shortest base \( BC\) is an isosceles triangle.

Solve also without using calculus (first derivative test).
It may be useful to remember the following formulas:

Carnot’s theorem (cosine formula)
Let \(\triangle ABC\) be a triangle with sides of length \(a,b,c\); then

\[ a^2 = b^2 + c^2 – 2bc \cos \alpha \]

where \( \alpha\) is opposite to the side of length \(a\). Similar formulas apply to the other two sides \(b,c\).

Area of ​​a triangle
The area of ​​a triangle with side lengths \(a,b,c\) is:

\[ S = \frac{bc \sin \alpha}{2} \]

where \( \alpha\) is opposite to the side of length \(a\). Similar formulas apply to the other two angles.